Setu Bridge of Pathway

 Chapter – 9: MECHANICAL PROPERTIES OF FLUIDS

Definition of Pressure :

Ø  Pressure means the force applied perpendicularly per unit area.

Ø  Pressure(P)=Force(F) / Area(A)

 

Ø  PressureSI unit of pressure is Pascal.

WHAT IS PASCAL’S LAW?

 Ø  Pascal's law states that any pressure applied to a fluid inside a closed system will transmit that pressure equally in all directions throughout the fluid. 

According to Pascal’s Law,

“The external static pressure applied on a confined liquid is distributed or transmitted evenly throughout the liquid in all directions”.

Pascal Law Formula

                F = PA

Where, 

F is the force applied,

P is the pressure transmitted,

A is the cross-sectional area.

Example of Pascal’s Law

Ø  A pressure of 2000 Pa is transmitted throughout a liquid column due to a force being applied on a piston. If the piston has an area of 0.1 m², what force is applied?

This can be calculated using Pascal’s Law formula.

F = PA

Here,

P = 2000 Pa = N/m²

A = 0.1 m²

Substituting values, we arrive at F = 200 N

Applications of Pascal’s Law

• Hydraulic Lift: The image you saw at the beginning of this article is a simple line diagram of a hydraulic lift. This is the principle of the working of hydraulic lift. It works based on the principle of equal pressure transmission throughout a fluid (Pascal’s Law).

·         Using Pascal’s Law various equipment are manufactured which are used in day to day life. 

·         Hydraulic jack and hydraulic press.

·         Hydraulic Brakes for increasing resisting force in the vehicle braking systems, Artesian wells, water towers, and dams.

·         Aircraft Hydraulic System: Hydraulic power systems in Aircraft use Pascal’s law to slow down aeroplanes on the runway. Also, used in flight control mechanisms, landing gears, etc.

·         Hydraulic Pumps: Hydraulic Pumps used in the Automobile industries uses the philosophy of Pascal’s Law.

·         Hydraulic testing of pressurised tanks, calibration of pressure gauges, pressing of oils such as olive, hazelnut, and sunflower oils, compression of wood stocks, etc.

Pascal’s Law Derivation

Consider an arbitrary right-angled prismatic triangle in the liquid of density rho. Since the prismatic element is very small, every point is considered to be at the same depth as the liquid surface. Therefore, T is also the same at all these points.

Let ad, bd, and cd be the area of the faces ABFE, ABDC, and CDFE, respectively.

Let P₁, P₂, and P₃ be the pressure on the faces ABFE, ABDC, and CDFE.

Pressure exerts a force which is normal to the surface. Let P₁ exert force F₁ on the surface ABFE, P₂ exert force F₂ on the surface ABDC, and P₃ exert force F₃ on the surface CDFE.

Therefore, Force F₁, F₂, and F₃ is given as:

F₁ = P₁ × area of ABFE = P₁ ad

F₂ = P₂ × area of ABDC = P₂ bd

F₃ = P₃ × area of CDFE = P₃ cd

Also,

Sinθ = b/a

Cosθ = c/a

The net force on the prism will be zero since the prism is in equilibrium.

F₁ sin θ = F₂
F₁ cos θ = F₃

P₁ ad b/a = P₂ bd (eq 1)
P₁ ad c/a = P₃ cd (eq 2)

From 1 and 2
P₁ = P₂ and P₁ = P₃

∴ P₁= P₂= P₃

_________________________________________________________________________________________________

Atmospheric Pressure

The atmospheric pressure at any point is measured as the weight of the column of air of unit cross-sectional area extended from the point under consideration to the top of the atmosphere. Using the same principle, a device was introduced by an Italian scientist Evangelista Torricelli, as shown in the figure below.

He took a long glass tube closed at one end and filled with mercury and inverted it into a trough of mercury. This device is termed as the mercury barometer. Here we can see that the space above the mercury column is filled with mercury vapours whose pressure is negligible, so it can well be considered a vacuum. Here, the pressure inside the column must be equal to the atmospheric pressure, as they are at the same level, so

Where, 

h is the height of the mercury column,

ρ is the density of the fluid,

P_a is the atmospheric pressure   (P_a = 1.01×10⁵ Pa)

g is the acceleration due to gravity.

• Atmospheric pressure is the pressure within the Earth’s atmosphere. The standard atmospheric pressure is 101,325 Pa.

 

In this experiment, the height of the mercury column was equal to 76 cm and thus, we commonly state the pressure in terms of cm or mm of mercury.

A manometer is a device that we use to measure the pressure of the pipelines (cab be of gas, water, liquid, etc.) Also, it is usually referred to as a U-shaped tube that is filled with a liquid.

What is Hydrostatic Paradox?

“The pressure at a certain horizontal level in the fluid is proportional to the vertical distance to the surface of the fluid.“

Ø  Examples of Hydrostatic Paradox

The concept can be appreciated through the following example:

Illustration of Hydrostatic Paradox: Four-vessel A, B, C and D of different shapes, containing a different volume of liquid, but all exert the same pressure (P) at all points at the same horizontal level.

They are connected to the common base by a horizontal pipe. On filling it with liquid, we can observe that; although the vessel’s shape varies, the horizontal liquid level in all vessels remains the same. The reason behind this mechanism is that the liquid pressure is the same at the bottom or in general, the fluid pressure is the same at all the points at the same depth

Fluid Pressure Formula

P= P_a + 𝝆gh 

• P is the pressure at depth “h” from the surface of the liquid/fluid.
• P_ais the atmospheric pressure.
• 𝝆 is the mass density of the fluid/liquid.
• g is the acceleration due to gravity.
• h is the vertical height from the surface to the point.

• Pascal(Pa) is the SI unit of pressure

Example :

What is the pressure on a swimmer at 10 m below the surface of a

Given:

• h = 10 m
• g = 9.8 m/s²
• 𝝆 = 1000 kg/m³
• P_a = 1.01×10⁵ Pa

 Solution:

1.      The pressure on a swimmer at 10 meters below the surface of a rectangularly shaped lake is

P= P_a + 𝝆gh

= 1.01×10⁵ Pa + 1000 kg/m³ × 9.8 m/s² × 10 m

= 199000 Pa

≅ 2 atm

WHAT ARE STREAMLINES?

Streamlines are defined as directly elected by the particles of the fluids below constant flow circumstances. If we constitute the flow lines with curves, Then the tangent drawn from any point on the curve tells us about the direction of the fluid velocity at the point given to us.

EXAMPLES OF STREAMLINED FLOW

·         Blood flow in veins

·         Water coming out from a tap

·         Smoke coming out from a cigarette till few centimeters

·         Water fountains placed in gardens

·         Flow in rivers and canals

·         Flow in water balloons

·         Aircraft flying at a constant speed

·         Viscous fluid like honey

BERNOULLI’S PRINCIPLE

Bernoulli’s principle formulated by Daniel Bernoulli states that as the speed of a moving fluid increases (liquid or gas), the pressure within the fluid decreases. Although Bernoulli deduced the law, it was Leonhard Euler who derived Bernoulli’s equation in its usual form in the year 1752.

“The total mechanical energy of the moving fluid comprising the gravitational potential energy of elevation, the energy associated with the fluid pressure and the kinetic energy of the fluid motion, remains constant.”

Bernoulli’s Principle Formula

Bernoulli’s equation formula is a relation between pressure, kinetic energy, and gravitational potential energy of a fluid in a container.

The formula for Bernoulli’s principle is given as follows:

Where,

p is the pressure exerted by the fluid,

v is the velocity of the fluid,

ρ is the density of the fluid and,

h is the height of the container.

Bernoulli’s Equation Derivation

Consider a pipe with varying diameter and height through which an incompressible fluid is flowing. The relationship between the areas of cross-sections A, the flow speed v, height from the ground y, and pressure p at two different points 1 and 2 are given in the figure below.

 

Assumptions:

• The density of the incompressible fluid remains constant at both points.
• The energy of the fluid is conserved as there are no viscous forces in the fluid.

 

 

Therefore, the work done on the fluid is given as:

dW = F₁dx₁ – F₂dx₂

dW = p₁A₁dx₁ – p₂A₂dx₂

dW = p₁dv – p₂dv = (p₁ – p₂)dv

We know that the work done on the fluid was due to the conservation of change in gravitational potential energy and change in kinetic energy. The change in kinetic energy of the fluid is given as:

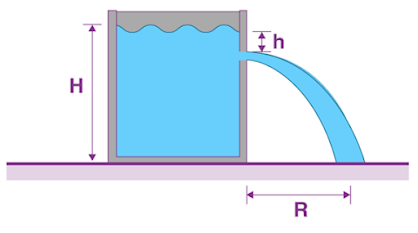
Example:

Calculate the pressure in the hose whose absolute pressure is 1.01 x 10⁵ N.m^-2 if the speed of the water in the hose increases from 1.96 m.s^-1 to 25.5 m.s^-1. Assume that the flow is frictionless and density 10³ kg.m^-3

Ans: Given,

Pressure at point 2, p₂ = 1.01 × 10⁵ N.m^-2 

Density of the fluid, ρ = 10³ kg.m^-3

Velocity of the fluid at point 1, v₁ = 1.96 m.s^-1

Velocity of the fluid at point 2, v₂ = 25.5 m.s^-1

 

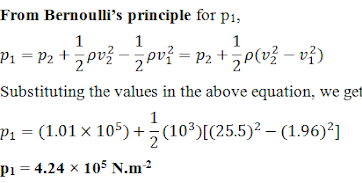
Applications of Bernoulli’s Principle

1)      Venturi meter: It is a device that is based on Bernoulli’s theorem and is used for measuring the rate of flow of liquid through the pipes. Using Bernoulli’s theorem, Venturi meter formula is given as:

2)      Working of an aeroplane: The shape of the wings is such that the air passes at a higher speed over the upper surface than the lower surface. The difference in airspeed is calculated using Bernoulli’s principle to create a pressure difference.

_________________________________________________________________________________

Torricelli's law

Torricelli’s law has practical applications in daily life. The physical law describes a major relationship between liquid exit velocity and its height in the container. 

Torricelli’s Law Derivation

Assuming that the fluid is incompressible, Bernoulli’s principle states that:

v²/2 + gh + P/ρ = constant

Where,

v is speed of liquid,

g denotes gravitational acceleration,

h shows liquid’s height over reference point,

ρ is density.

P is equal to atmospheric pressure at the top of the container.

Ø  “v” is considered as “0” because the liquid surface drops in height slowly compared to the speed at which liquid leaves the tank.

Ø  “h” is 0 and “p” is atmospheric pressure at opening h = 0.

v² = 2gh

V = √ (2gh)

THE DEFINITION OF VISCOSITY IS AS FOLLOWS:

“Viscosity is a measure of a fluid’s resistance to flow”.

The SI unit of viscosity is poiseiulle (PI).

 Its other units are newton-second per square metre (N s m^-2) or pascal-second (Pa s.)

The dimensional formula of viscosity is [ML^-1T^-1].

Ø  Viscosity Formula

Viscosity is measured in terms of a ratio of shearing stress to the velocity gradient in a fluid. If a sphere is dropped into a fluid, the viscosity can be determined using the following formula:

Ø  Viscosity Types

Viscosity is the measure of fluid’s friction to its flow. There are two ways to measure the fluid’s viscosity as follows:

1.Dynamic Viscosity (Absolute Viscosity)

2. Kinematic Viscosity

 

Q1 What is Viscosity?

Viscosity is a measure of a fluid’s resistance to flow.

Q2 Why is viscosity an intensive property?

Viscosity does not change as the amount of matter changes, therefore it is an intensive property.

Q3 How does viscosity vary with temperature?

The viscosity of liquids decreases rapidly with an increase in temperature, and the viscosity of gases increases with an increase in temperature.

Q4 How are viscosity and flow rate related?

As the viscosity increases, the flow rate decreases. The flow rate is inversely proportional to viscosity.

Q5 What is Kinematic Viscosity?

Kinematic viscosity is a measure of a fluid’s internal resistance to flow under gravitational forces.

_______________________________________________________________________

EXCESS PRESSURE INSIDE CURVED SURFACE- LIQUID DROP, AIR BUBBLE AND SOAP BUBBLE

 

 

Types of Surface 

The bubbles, such as soap bubbles, are like blown-up balloons, air inside and air outside with a thin liquid film in between them. This thin film naturally has two free surfaces, one inside and the other outside. In most cavities, there is air inside and liquid outside. They only have one free surface or interface. Water or another liquid is usually found inside drops, whereas air or another gas is found outside. They have one visible surface as well.

Plane Surface
If the surface of the liquid is plane as shown in the figure, the molecule on the liquid surface is attracted equally in all directions. The resultant force due to surface tension is zero. The pressure, therefore, on the liquid surface is perpendicular. 

 

Concave Surface
If the surface is concave upwards as shown in the figure. Since there will be upward resultant force due to surface tension acting on the molecule. As the molecule on the surface is in equilibrium, there must be an excess of pressure on the concave side. 

 

Convex Surface
If the surface is convex as shown in figure. The resultant force due to surface tension acts in the downward direction. Since the molecules on the surface are in equilibrium, there must be an excess of pressure on the concave side of the surface acting in the upward direction to balance the downward resultant force of surface tension. Hence, there is always an excess of pressure on the concave side of a curved surface over that on the convex side

Excess Pressure Inside Liquid Drop or Air Bubble

The magnitude of excess pressure can be obtained by studying the formation of air and soap bubbles. Liquid drop and Air bubble have a single surface so both have the same excess pressure inside. So the following results will be the same for both liquid drop and air bubble.

Figure below shows the one-half cross section of an air bubble formed inside liquid. It is an equilibrium under the action of three forces:

Due to external pressure (P₁)

Due to internal pressure (P₂)

Due to surface tension of liquid (T)

If R is the radius of air bubble, then the forces due to external and internal pressure are

Projected area will form a circle of radius R, so 

So, 

and 
will be two forces because of external pressure and internal pressure respectively. Since the surface tension acts around the circumference of the bubble and there is single surface, therefore the force of surface tension is 

Thus from condition of equilibrium,

Excess Pressure Inside Soap Bubble

A soap bubble forms two liquid surfaces in contact with air, one inside the bubble other outside the bubble. Figure below shows the one-half cross section of the soap bubble. 

As soap bubble forms two liquid surfaces, force because of surface tension is

By considering its equilibrium we get,

Q1. The surface tension of a soap solution is What is the extra pressure within a 1cm soap bubble?

Answer: Excess pressure is calculated as,

 

Q2. The air pressure of soap bubble is 8 mm of water above atmospheric pressure. If radius of bubble is 0.35 cm then find the surface tension of the soap solution?

Answer: Excess pressure is calculated as,

 

Q1 What is surface tension?

Surface tension is the tension of the surface film of a liquid caused by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimise surface area

Q2 What is cohesion?

When two similar substances or molecules face the force of attraction this force is known as cohesion force. Water is an example of cohesion. Each water molecule forms hydrogen bonds with neighbouring molecules.

Q3 What is adhesion?

When two dissimilar substances or molecules face the force of attraction this force is known as adhesion force. Water drops on the surface of leaves and flowers.

Q4 Define pressure.

The force applied perpendicular to the surface of an object per unit area over which that force is distributed is known as pressure.

Q5 What is capillary action?

We can define capillary action as a phenomenon where ascension of liquids through a tube or cylinder takes place. This primarily occurs due to adhesive and cohesive forces.